Building Java Programs
Lab: Advanced Data Structures
Except where otherwise noted, the contents of this document are Copyright 2019 Stuart Reges and Marty Stepp.
Lab goals
Goals for this problem set:
- Learn about hash tables and heaps
- Examine hash functions and how they map elements to array indexes
- Practice adding and removing elements from a heap
- Use heaps to implement priority queue operations
Hash tables
hash table: An array that stores elements in it using a hash function that maps values to indexes.
- most common hash function: n → n
%length - benefits: O(1) very fast add/lookup speed!
- collision: When two values map to the same hash index.
- Example: 87 and 37 both hash to the index 7 below.
- linear probing: Resolve collisions by moving forward to the next available index.
- Example: If index 7 already occupied by 87, put 37 at next index 8.
Example: hash table of length 10. Add values 87, 12, 37, 54.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 12 |
54 |
87 |
37 |
Exercise : hashTableAdd
What is the final state of a hash table array of size 10 after adding 35, 2, 15, 80, 42, 95, and 66? Assume that we are using the standard "mod" hash function shown in the chapter and linear probing for collision resolution. Do not perform any resizing or rehashing.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 80 | 0 | 2 | 42 | 0 | 35 | 15 | 95 | 66 | 0 |
Exercise : hashMapAdd
Write the final state of the hash map after the following key/value pairs are added and removed.
Assume that it uses the standard "mod" hash function shown in the chapter and uses linear probing for collision resolution.
Write each pair in key=value format, or X in any index in which an element is removed and not replaced by another element.
Do not perform any resizing or rehashing.
HashMap<Integer, String> map = new HashMap<Integer, String>(); map.put(8, "Q"); map.put(27, "J"); map.put(34, "T"); map.put(57, "R"); map.put(45, "Y"); map.put(74, "S"); map.put(27, "M"); map.put(95, "K"); map.remove(74); map.put(76, "T"); map.remove(8); map.remove(5); map.put(14, "D");
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 45=Y | 27=M | X |
| index | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 34=T | 14=D | 95=K | 57=R | 76=T |
HashIntSet
In this chapter we develop a class HashIntSet that uses a hash table to store a set of integers:
The class uses the following data fields (refer to them in your exercise solutions):
public class HashIntSet {
private HashEntry[] elementData; // hash table
private int size;
...
}
Each index ("bucket") of the hash table stores a linked list of hash entry objects (null if empty):
public class HashEntry {
public int data;
public HashEntry next;
...
Exercise : containsAll

Write a method in the HashIntSet class called containsAll that accepts another hash set as a parameter and returns true if your set contains every element from the other set.
For example, if the set stores [-2, 3, 5, 6, 8] and the method is passed [3, 6, 8], your method would return true.
If the method were passed [3, 6, 7, 8], your method would return false because your set does not contain the value 7.
Exercise : retainAll

Write a method in the HashIntSet class called retainAll that accepts another hash set as a parameter and removes all elements from this set that are not contained in the other set.
For example, if the set stores [-2, 3, 5, 6, 8] and the method is passed [2, 3, 6, 8, 11], your set would store [3, 6, 8].
Heaps
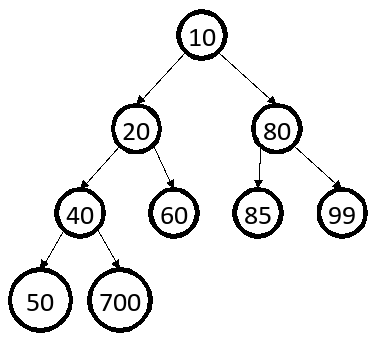
heap: A complete binary tree with vertical ordering. Internal data structure used to implement a priority queue.
- complete tree: Every level is full except possibly the lowest level, which must be filled from left to right (i.e., a node may not have any children until all possible siblings exist)
- heap ordering: If P = X for every element X with parent P.
- Parents' values are always smaller than those of their children.
- Implies that minimum element is always the root (a "min-heap").
- A "max-heap" stores largest element at root, reverses ordering.
Adding to a Heap
- When an element is added to a heap, it should be initially placed as the rightmost leaf (to maintain the completeness property).
- bubble up: To restore heap ordering, the newly added element is shifted ("bubbled") up the tree by swapping with its parent until it reaches its proper sorted place.
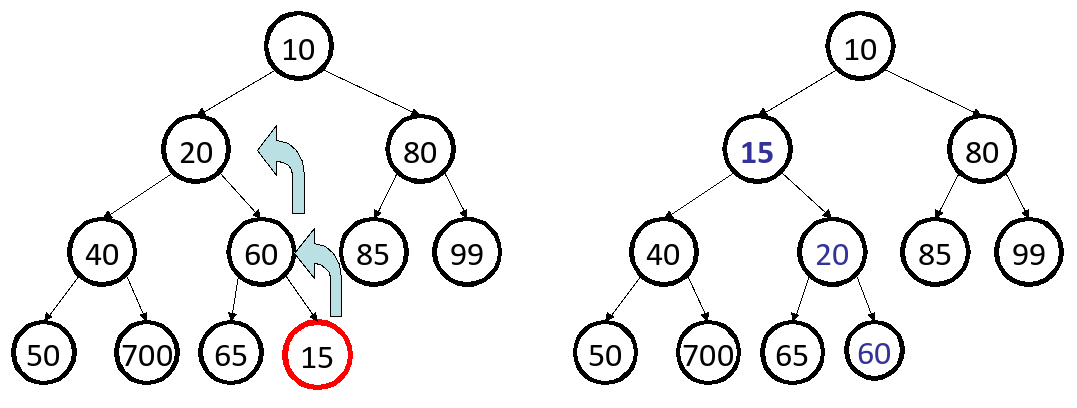
Exercise : heapAdd
Draw the tree for the binary min-heap that results from inserting these elements in this order into an initially empty heap: 11, 9, 12, 14, 3, 15, 7, 8, 1
| 1 | ||||||||||||
| / | \ | |||||||||||
| 3 | 7 | |||||||||||
| / | \ | / | \ | |||||||||
| 8 | 11 | 15 | 12 | |||||||||
| / | \ | |||||||||||
| 14 | 9 |
Priority Queues
priority queue: A collection of ordered elements that provides fast access to the minimum (or maximum) element. Often implemented using a heap internally. Common operations:
pq.add(value);: adds in orderpq.peek(): returns minimum or "highest priority" valuepq.remove(): removes/returns minimum valuepq.isEmpty(),pq.size(),pq.clear();,pq.iterator(): all O(1) runtime
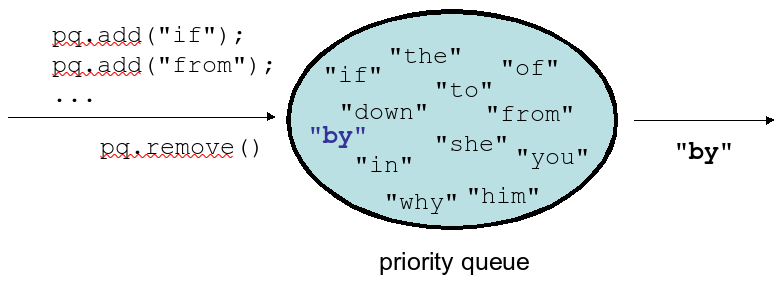
Exercise : kthSmallest

Write a method called kthSmallest that accepts a PriorityQueue of integers and an integer k as parameters and returns the kth-smallest integer from the priority queue (where k=1 would represent the very smallest).
For example, if the queue passed stores the integers [42, 50, 45, 78, 61] and k is 4, return the fourth-smallest integer, which is 61.
If k is 0 or negative or greater than the size of the queue, throw an IllegalArgumentException.
If your method modifies the state of the queue during its computation, it should restore the queue before it returns.
You may use one stack or queue as auxiliary storage.
Exercise : stutter

Write a method called stutter that accepts a PriorityQueue of integers as a parameter and replaces every value in the queue with two occurrences of that value.
For example, if the queue stores [7, 8, 10, 45], your method should modify the queue to store [7, 7, 8, 8, 10, 10, 45, 45].
You may use one stack or queue as auxiliary storage.
Exercise : removeDuplicates

Write a method called removeDuplicates that accepts a PriorityQueue of integers as a parameter and modifies the queue's state so that any element that is equal to another element in the queue is removed.
For example, if the queue stores [7, 7, 8, 8, 8, 10, 45, 45], your method should modify the queue to store [7, 8, 10, 45].
You may use one stack or queue as auxiliary storage.