Binary trees
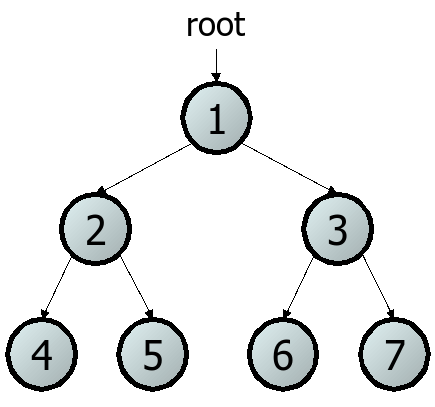
binary tree: A directed, acyclic structure of linked nodes where each node has at most two children.
- directed: Has one-way links between nodes.
- acyclic: No path wraps back around to the same node twice.
Common tree terminology:
- node: an object containing a data value and left/right children
- root: topmost node of a tree
- leaf: a node that has no children
- branch: any internal node; neither the root nor a leaf
- parent: a node that refers to this one
- child: a node that this node refers to
- siblings: nodes with a common parent
Exercise : traversals1
Write the elements of the tree below in the order they would be seen by a pre-order (root-left-right), in-order (left-root-right), and post-order (left-right-root) traversal, separated by spaces.
+---+
| 3 |
+---+
/ \
+---+ +---+
| 5 | | 2 |
+---+ +---+
/ / \
+---+ +---+ +---+
| 1 | | 4 | | 6 |
+---+ +---+ +---+
- pre-order: 3 5 1 2 4 6
- in-order: 1 5 3 4 2 6
- post-order: 1 5 4 6 2 3
Exercise : traversals2
Write the elements of the tree below in the order they would be seen by a pre-order (root-left-right), in-order (left-root-right), and post-order (left-right-root) traversal, separated by spaces.
+----+
| 19 |
+----+
/ \
+----+ +----+
| 47 | | 63 |
+----+ +----+
/ \ \
+----+ +----+ +----+
| 23 | | -2 | | 94 |
+----+ +----+ +----+
/ \
+----+ +----+
| 55 | | 28 |
+----+ +----+
- pre-order: 19 47 23 -2 55 63 94 28
- in-order: 23 47 55 -2 19 63 94 28
- post-order: 23 55 -2 47 28 94 63 19
IntTree.java
Here is the code for IntTree as written in this chapter:
IntTree.javaThe class uses the following data field (refer to it in your exercise solutions):
public class IntTree {
private IntTreeNode overallRoot; // null if empty
...
}
public class IntTreeNode {
public int data; // data stored in this node
public IntTreeNode left; // link to left child of this node (null if none)
public IntTreeNode right; // link to right child of this node (null if none)
...
}
Exercise : countLeftNodes
Write a method countLeftNodes that could be added to the IntTree class.
Your method should return the number of left children in the tree.
A left child is a node that appears as the root of the left-hand subtree of another node.
An empty tree has 0 left nodes.
For example, if an IntTree variable tree refers to the following tree, the call of tree.countLeftNodes() should return 4 because the tree has four left children (the nodes storing the values 5, 1, 4, and 7).
+---+
| 3 |
+---+
/ \
+---+ +---+
| 5 | | 2 |
+---+ +---+
/ / \
+---+ +---+ +---+
| 1 | | 4 | | 6 |
+---+ +---+ +---+
/
+---+
| 7 |
+---+
Exercise : printLeaves
Write a method printLeaves that could be added to the IntTree class.
Your method should output to the console the values of the leaves of the binary tree from right to left.
More specifically, the leaves should be printed in the reverse order that they would be printed using any of the standard traversals.
For example, if an IntTree variable tree refers to the following tree, the call of tree.printLeaves(); should print the following console output:
+---+
| 2 |
+---+
/ \
+---+ +---+
| 8 | | 1 |
+---+ +---+
/ / \
+---+ +---+ +---+
| 0 | | 7 | | 6 |
+---+ +---+ +---+
/ \
+---+ +---+
| 4 | | 9 |
+---+ +---+
leaves: 9 4 0
If the tree does not have any leaves (an empty tree), simply print: no leaves
Exercise : depthSum
Write a method depthSum that could be added to the IntTree class.
Your method should return the sum of the values stored in a binary tree of integers weighted by the depth of each value.
You should return the value at the overallRoot, plus 2 times the values stored at the next level of the tree, plus 3 times the values stored at the next level of the tree, plus 4 times the values stored at the next level of the tree, and so on.
For example, if an IntTree variable tree refers to the following tree, the call of tree.depthSum() would return 90, which would be computed as follows:
+---+
| 9 |
+---+
/ \
+---+ +---+
| 7 | | 6 |
+---+ +---+
/ \ \
+---+ +---+ +---+
| 3 | | 2 | | 4 |
+---+ +---+ +---+
/ \
+---+ +---+
| 5 | | 2 |
+---+ +---+
1 * 9 + 2 * (7 + 6) + 3 * (3 + 2 + 4) + 4 * (5 + 2) = 90
Exercise : removeLeaves
Write a method removeLeaves that could be added to the IntTree class.
Your method should remove all leaves from the tree.
A leaf node that has empty left and right subtrees.
For example, if an IntTree variable tree refers to the tree at left below, the call of tree.removeLeaves(); should remove the four leaves from the tree (the nodes with data values 1, 4, 6, and 0) leaving the tree shown at right.
| Before | After |
|---|---|
+---+
| 7 |
___ +---+ ___
/ \
+---+ +---+
| 3 | | 9 |
+---+ +---+
/ \ / \
+---+ +---+ +---+ +---+
| 1 | | 4 | | 6 | | 8 |
+---+ +---+ +---+ +---+
\
+---+
| 0 |
+---+
|
+---+
| 7 |
+---+
/ \
+---+ +---+
| 3 | | 9 |
+---+ +---+
\
+---+
| 8 |
+---+
|
Exercise : completeToLevel
Write a method completeToLevel that could be added to the IntTree class.
Your method should accept an integer n as a parameter and add nodes to the tree so that the first n levels are complete.
A level is complete if every possible node at that level is not null.
We will use the convention that the overall root is at level 1, its children are at level 2, and so on.
You should preserve any existing nodes in the tree.
Any new nodes added to the tree should have -1 as their data.
For example, if an IntTree variable tree refers to the tree at left below, the call of tree.completeToLevel(3); should modify the tree's state to be that at right after the call:
| Before | After |
|---|---|
+----+
| 17 |
+----+
/ \
+----+ +----+
| 83 | | 6 |
+----+ +----+
/ \
+----+ +----+
| 19 | | 87 |
+----+ +----+
\ /
+----+ +----+
| 48 | | 75 |
+----+ +----+
|
+----+
| 17 |
_______+----+_______
/ \
+----+ +----+
| 83 | | 6 |
+----+ +----+
/ \ / \
+----+ +----+ +----+ +----+
| 19 | | -1 | | -1 | | 87 |
+----+ +----+ +----+ +----+
\ /
+----+ +----+
| 48 | | 75 |
+----+ +----+
|
Keep in mind that your method might need to fill in several different levels.
Your method should throw an IllegalArgumentException if passed a value for level that is less than 1.
Exercise : trim
Write a method trim that could be added to the IntTree class.
Your method should accept minimum and maximum integers as parameters and remove from the tree any elements that are not within that range, inclusive.
For this method you should assume that your tree is a binary search tree (BST) and that its elements are in valid BST order, meaning that left children have values smaller than their parents, and right children have values larger than their parents.
Your method should maintain the BST ordering property of the tree.
For example, if an IntTree variable tree refers to the tree at left below, the call of tree.trim(25, 72); should modify the tree's state to be that at right after the call:
| Before | After |
|---|---|
+----+
| 50 |
_____ +----+ _____
/ \
+----+ +----+
| 38 | | 90 |
_____ +----+ ___ +----+
/ \ /
+----+ +----+ +----+
| 14 | | 42 | | 54 |
+----+ +----+ +----+
/ \ \
+----+ +----+ +----+
| 8 | | 20 | | 72 |
+----+ +----+ +----+
\ / \
+----+ +----+ +----+
| 26 | | 61 | | 83 |
+----+ +----+ +----+
|
+----+
| 50 |
_ +----+
/ \
+----+ +----+
| 38 | | 54 |
+----+ +----+
/ \ \
+----+ +----+ +----+
| 26 | | 42 | | 72 |
+----+ +----+ +----+
/
+----+
| 61 |
+----+
|
The BST ordering property is important for solving this problem. If a node's data value is too large or too small to fit within the range, this may also tell you something about whether that node's left or right subtree elements can be within the range. Taking advantage of such information makes it more feasible to remove the correct nodes.