Building Java Programs

Lab: Stacks and Queues

Except where otherwise noted, the contents of this document are Copyright 2019 Stuart Reges and Marty Stepp.

Lab goals

Goals for this problem set:

• practice using stacks
• practice using queues
• practice using stacks and queues together

Stacks

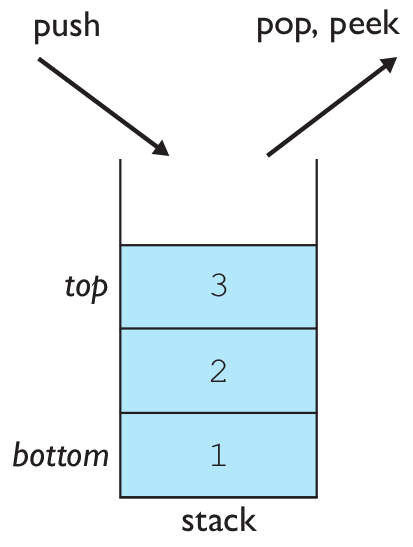
stack: A collection based on the principle of adding elements and retrieving them in the opposite order. This is called Last-In, First-Out ("LIFO").

Basic stack operations:

• push: Add an element to the top.
• pop: Remove the top element.
• peek: Examine the top element.

Exercise : stackMystery

What output is produced by the following code?

Stack<Integer> s = new Stack<Integer>();
s.push(7);
s.push(10);
System.out.print(s.peek() + " ");
System.out.print(s.pop() + " ");
s.push(3);
s.push(5);
System.out.print(s.pop() + " ");
System.out.print(s.size() + " ");
System.out.print(s.peek() + " ");
s.push(8);
System.out.print(s.pop() + " ");
System.out.print(s.pop());

• 10 10 5 2 3 8 3

Exercise : stutter

Write a method stutter that takes a stack of integers as a parameter and replaces every value in the stack with two occurrences of that value. For example, suppose the stack named s stores these values:

bottom [3, 7, 1, 14, 9] top

Then the stack should store these values after the call of stutter(s):

bottom [3, 3, 7, 7, 1, 1, 14, 14, 9, 9] top

Notice that you must preserve the original order. You may use a single queue as auxiliary storage to solve this problem.

Exercise : equals

Write a method equals that takes as parameters two stacks of integers and returns true if the two stacks are equal and false otherwise. To be considered equal, the two stacks would have to store the same sequence of integer values in the same order. Your method is to examine the two stacks but must return them to their original state before terminating. You may use one stack as auxiliary storage.

Queues

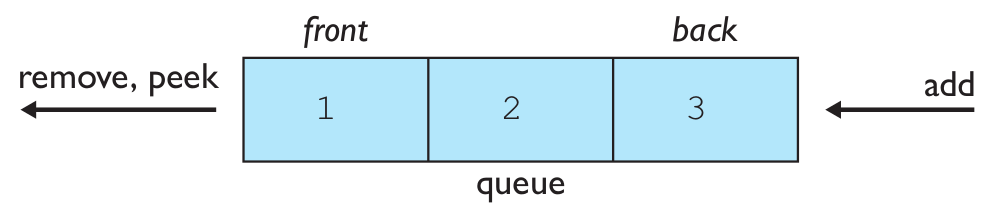
queue: Retrieves elements in the order they were added. This is called First-In, First-Out ("FIFO").

Basic queue operations:

• add (enqueue): Add an element to the back.
• remove (dequeue): Remove the front element.
• peek: Examine the front element.

Exercise : queueMystery

What output is produced by the following code? Note: A Queue prints in the format [a, b, c] from front to back.

Queue<Integer> queue = new LinkedList<Integer>();
for (int i = 1; i <= 6; i++) {
    queue.add(i);
}

for (int i = 0; i < queue.size(); i++) {
    System.out.print(queue.remove() + " ");
}
System.out.print(queue + " size " + queue.size());

• 1 2 3 [4, 5, 6] size 3

Exercise : isPalindrome

Write a method isPalindrome that accepts a queue of integers as a parameter and returns true if the numbers in the queue are the same in reverse order. For example, if the queue stores [3, 8, 17, 9, 17, 8, 3], your method should return true because this sequence is the same in reverse order. If the queue stores [3, 17, 9, 4, 17, 3], your method would return false because this sequence is not the same in reverse order (the 9 and 4 in the middle don't match). The empty queue should be considered a palindrome. Your method must restore the parameter queue to its original state before returning. Use one stack as auxiliary storage.

Exercise : reorder

Write a method reorder that accepts a queue of integers as a parameter and that puts the integers into sorted (nondecreasing) order, assuming that the queue is already sorted by absolute value. For example, if the queue stores [1, 2, -2, 4, -5, 8, -8, 12, -15], notice that the values appear in sorted order if you ignore the sign of the numbers. Your method should reorder the values so that the queue stores [-15, -8, -5, -2, 1, 2, 4, 8, 12]. Use one stack as auxiliary storage.

Exercise : interleave

Write a method interleave that accepts a queue of integers as a parameter and rearranges the elements by alternating the elements from the first half of the queue with those from the second half of the queue. For example, if the queue stores [2, 8, -5, 19, 7, 3, 24, 42], your method should change it to store [2, 7, 8, 3, -5, 24, 19, 42]. To understand the result, consider the two halves of this queue. The first half is [2, 8, -5, 19] and the second half is [7, 3, 24, 42]. These are combined in an alternating fashion to form a sequence of pairs: the first values from each half (2 and 7), then the second values from each half (8 and 3), and so on. Throw an IllegalArgumentException if the queue does not have an even size. Use one stack as auxiliary storage.

Exercise : removeMin

Write a method removeMin that accepts a stack of integers as a parameter and removes and returns the smallest value from the stack. For example, if the stack stores [2, 8, 3, 19, 2, 3, 2, 7, 12, -8, 4], your method should remove and return -8, leaving the stack storing [2, 8, 3, 19, 2, 3, 2, 7, 12, 4]. If the minimum value appears more than once, all occurrences of it should be removed. For example, given the same stack, if we again call removeMin on it, the method would return 2 and leave the stack storing [8, 3, 19, 3, 7, 12, 4]. Use one queue as auxiliary storage.